
Chapter 9
Infinite Series
Infinite sequences and series may converge or diverge. In this chapter, we will look at methods to determine the convergence and divergence.
Chapter 9.1
Sequences
-
sequence - a function whose domain is the set of positive integers
Although a sequence is a function, it is common to represent sequences by subscript notation rather than by the standard function notation. For instance, in the sequence
1, 2, 3, 4, … n, …
1 -> a-^1
2 -> a-^2
3 -> a-^3
4 -> a-^4
…
n -> a-^n
…
1 is mapped onto a-^1, 2 is mapped onto a-^2, and so on.
-
The numbers a-^1, a-^2, a-^3, … a-^n, … are the terms of the sequence.
-
The number a-^n is the nth term of the sequence.
-
The entire sequence is denoted by {a-^n}.
-
recursively defined sequence:
Example: {d-^n}: d-^(n + 1) = d-^n - 5
Definition of the Limit of a Sequence:
Let L be a real number. The limit of a sequence {a-^n} is L, written as
lim (-^- (x -> ∞)) a-^n = L
if for each ε > 0, there exists M > 0 such that |a-^n - L| < ε whenever n > M. If the limit L of a sequence exists, then the sequence converges to L. If the limit of a sequence does not exist, then the sequence diverges.
Graphically, this definition says that eventually the terms of a series that converge to L will lie within the band between the lines y = L + ε and y = L - ε.


Theorem 9.1 - Limit of a Sequence:
Let L be a real number. Let f be a function of a real variable such that
lim (-^- (x -> ∞)) f(x) = L
If {a-^n} is a sequence such that f(n) = a-^n for every positive integer n, then
lim (-^- (x -> ∞)) a-^n = L
Theorem 9.2 - Properties of Limits of Sequences:
Let lim (-^- (x -> ∞)) a-^n = L and lim (-^- (x -> ∞)) b-^n = K
1. lim (-^- (x -> ∞)) (a-^n ± b-^n) = L ± K
2. lim (-^- (x -> ∞)) ca-^n = cL
(c is any real number)
3. lim (-^- (x -> ∞)) (a-^n * b-^n) = LK
4. lim (-^- (x -> ∞)) (a-^n / b-^n) = L/K
(b-^n ≠ 0 and K ≠ 0)
-
n factorial - n! = 1 * 2 * 3 * 4 * … * (n - 1) * n
-
zero factorial - 0! = 1
NOTE: Factorials follow the same conversions for order of operations as exponents:
2n! = 2(n!) = 2(1 * 2 * 3 * … * n)
(2n)! = 1 * 2 * 3 * … * n * (n + 1) * … * 2n
Theorem 9.3 - Squeeze Theorem for Sequences:
If
lim (-^- (x -> ∞)) a-^n
= lim (-^- (x -> ∞)) b-^n
= L
and there exists an integer N such that a-^n ≤ c-^n ≤ b-^n for all n > N, then
lim (-^- (x -> ∞)) c-^n = L
Theorem 9.4 - Absolute Value Theorem:
For the sequence {a-^n}, if
lim (-^- (x -> ∞)) |a-^n| = 0
then
lim (-^- (x -> ∞)) a-^n = 0
Proof: Consider the two sequences {|a-^n|} and {-|a-^n|}. Because both of these sequences converge to 0 and
-|a-^n| ≤ a-^n ≤ |a-^n|
you can use the Squeeze Theorem to conclude that {a-^n} converges to 0.
Definition of a Monotonic Sequence:
A sequence {a-^n} is monotonic if its terms are nondecreasing
a-^1 ≤ a-^2 ≤ a-^3 ≤ … ≤ a-^n ≤ …
or if its terms are nonincreasing
a-^1 ≥ a-^2 ≥ a-^3 ≥ … ≥ a-^n ≥ …
Definition of a Bounded Sequence:
1. A sequence {a-^n} is bounded above if there is a real number M such that a-^n ≤ M for all n. The number M is called an upper bound of the sequence.
2. A sequence {a-^n} is bounded below if there is a real number N such that N ≤ a-^n for all n. The number N is called a lower bound of the sequence.
3. A sequence {a-^n} is bounded if it is bounded above and bounded below.
-
One important property of the real numbers is that they are complete. (There are no holes or gaps on the real number line.)
-
The completeness axiom for real numbers can be used to conclude that if a sequence has an upper bound, it must have a least upper bound (an upper bound that is smaller than all the other upper bounds for the sequence).
Example: {a-^n} = {n/(n + 1)}
(1/2), (2/3), (3/4), (4/5), … , (n/(n +1), …
least upper bound = 1
Theorem 9.5 - Bounded Monotonic Sequences:
If a sequence {a-^n} is bounded and monotonic, then it converges.
Chapter 9.2
Series and Convergence
If {a-^n} is an infinite sequence, then
(∞) Σ (n = 1) a-^n = a-^1 + a-^2 + a-^3 + … + a-^n + …
is an infinite series (or simply a series). The numbers a-^1, a-^2, a-^3, are the terms of the series
-
For some series, it is convenient to begin the index at n = 0 (or another integer).
-
As a typesetting convention, it is common to represent an infinite series as simply Σ a-^n.
To find the sun of an infinite series, consider the following sequence of partial sums.
S-^1 = a-^1
S-^2 = a-^1 + a-^2
S-^3 = a-^1 + a-^2 + a-^3
…
S-^n = a-^1 + a-^2 + a-^3 + … + a-^n
Definition of Convergent and Divergent Series:
For the infinite series (∞) Σ (n = 1) a-^n, the nth partial sum is given by
S-^n = a-^1 + a-^2 + a-^3 + … + a-^n
If the sequence of partial sums {S-^n} converges to S, then the series (∞) Σ (n = 1) a-^n converges. The limit S is called the sum of the series.
S = a-^1 + a-^2 + a-^3 + … + a-^n + …
If {S-^n} diverges, then the series diverges.
-
telescoping series - will converge if and only if b-^n approaches a finite number as n -> ∞
Example:
(b-^1 - b-^2) + (b-^2 - b-^3) + (b-^3 - b-^4) …
nth partial sum: S-^n = b-^1 - b-^(n + 1)
sum: S = b-^1 - lim (-^- (x -> ∞)) b-^(n + 1)
-
To write a series in telescoping form, use partial fractions.
-
geometric series - the series given by
(∞) Σ (n = 0) ar^n
= a + ar + ar^2 + … + ar^n + …
a ≠ 0
is a geometric series with ratio r.
Theorem 9.6 - Convergence of a Geometric Series:
A geometric series with ratio r diverges if |r| ≥ 1. If 0 < |r| < 1, then the series converges to the sum
(∞) Σ (n = 0) ar^n
= (∞) Σ (n = 1) ar^(n - 1)
= a-^1/(1 - r)
This is also know as the geometric series test (GST).
Theorem 9.7 - Properties of Infinite Series:
If Σ a-^n = A, Σ b-^n = B, and c is a real number, then the following series converge to the indicated sums.
1. (∞) Σ (n = 1) ca-^n = cA
2. (∞) Σ (n = 1) (a-^n + b-^n) = A + B
3. (∞) Σ (n = 1) (a-^n - b-^n) = A - B
Theorem 9.8 - Limit of nth Term of a Convergent Series:
If (∞) Σ (n = 1) a-^n converges, then lim (-^- (x -> ∞)) a-^n = 0
Theorem 9.9 - nth Term Test for Divergence:
If lim (-^- (x -> ∞)) a-^n ≠ 0, then (∞) Σ (n = 1) a-^n diverges.
Chapter 9.3
The Integral Test and p-Series
Theorem 9.10 - The Integral Test:
If f is positive, continuous, and decresing for x ≥ 1 and a-^n = f(n), then
(∞) Σ (n = 1) a-^n
and
(∫ a->b) f(x) dx
either both converge or diverge.
-
p-series - a series of the form
(∞) Σ (n = 1) 1/(n^p)
= (1/1^p) + (1/2^p) + (1/3^p) + …
p is a positive constant
-
For p = 1, the series
(∞) Σ (n = 1) 1/n
= 1 + (1/2) + (1/3) + …
is the harmonic series. A general harmonic series is of the form Σ 1/(an + b)
Theorem 9.11 - Convergence of p-Series:
The p-series
(∞) Σ (n = 1) 1/(n^p)
= (1/1^p) + (1/2^p) + (1/3^p) + …
1. converges if p > 1
2. diverges if 0 < p ≤ 1
This is also known as the p-series test (PST).
Chapter 9.4
Comparison of Series
-
A slight deviation from certain special characteristics can make a test nonapplicable, but there are comparison tests to help with the determination of convergence and divergence.
Theorem 9.12 - Direct Comparison Test (DCT):
Let 0 < a-^n ≤ b-^n for all n.
1. If (∞) Σ (n = 1) b-^n converges, then (∞) Σ (n = 1) a-^n converges.
2. If (∞) Σ (n = 1) a-^n diverges, then (∞) Σ (n = 1) b-^n diverges.
Theorem 9.13 - Limit Comparison Test (LCT):
Suppose that a-^n > 0, b-^n > 0, and
lim (-^- (x -> ∞)) (a-^n/b-^n)
= L
where L is finite and positive. Then the two series Σ a-^n and Σ b-^n either both converge or both diverge.
Chapter 9.5
Alternating Series
-
alternating series - contains terms that alternate in sign; occurs in two ways: either the odd terms are negative or the even terms are negative
Theorem 9.14 - The Alternate Series Test (AST):
Let a-^n > 0. The alternating series
(∞) Σ (n = 1) (-1)^n * a-^n
and
(∞) Σ (n = 1) (-1)^(n + 1) * a-^n
converge if the following two conditions are met
1. lim (-^- (x -> ∞)) a-^n = 0
2. a-^(n + 1) ≤ a-^n, for all n
Theorem 9.15 - Alternating Series Remainder:
If a convergent alternating series satisfies the condition a-^(n + 1) ≤ a-^n, then the absolute value of the remainder R-^N involved in approximating the sum S by S-^N is less than (or equal to) the first neglected term. That is
|S - S-^N| = |R-^N| ≤ a-^(N + 1)
NOTE: If the series converge without the alternating piece, then it will converge with the alternating piece.
Theorem 9.16 - Absolute Convergence:
If the series Σ |a-^n| converges, then the series Σ a-^n also converges.
NOTE: The converse of Theorem 9.16 is not true. The alternating harmonic series
(∞) Σ (n = 1) (-1)^(n + 1) / n
= (1/1) - (1/2) + (1/3) - (1/4) + …
converges by the Alternating Series Test. Yet the harmonic series diverges. This type of convergence is called conditional convergence.
Definitions of Absolute and ConditionalConvergence:
1. Σ a-^n is absolutely convergent if Σ |a-^n| converges.
2. Σ a-^n is conditionally convergent if Σ a-^n converges but Σ |a-^n| diverges.
Chapter 9.6
The Ratio and Root Tests
Theorem 9.17 - Ratio Test:
Let Σ a-^n be a series with nonzero terms.
1. Σ a-^n converges absolutely if lim (-^- (x -> ∞)) |(a-^(n + 1)) / (a-^n)| < 1
2. Σ a-^n diverges if lim (-^- (x -> ∞)) |(a-^(n + 1)) / (a-^n)| > 1
or lim (-^- (x -> ∞)) |(a-^(n + 1)) / (a-^n)|= ∞
3. The Ratio Test is inconclusive if lim (-^- (x -> ∞)) |(a-^(n + 1)) / (a-^n)|= 1
NOTE: The Ratio Test is good for factorials and exponentials.
Theorem 9.18 - Root Test:
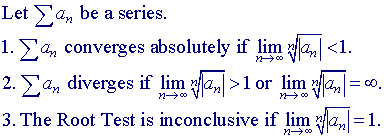
NOTE: The Root Test is useful when sequence terms can be written to the nth power.
Guidelines for Testing a Series for Convergence or Divergence:
1. Does the nth term approach 0? If not, the series diverges.
2. Is the series one of the special types — geometric, p-series, telescoping, or alternating?
3. Can the Integral Test, the Root Test, or the Ratio Test be applied?
4. Can the series be compared favorably to one of the special types?

Chapter 9.7
Taylor Polynomials and Approximations
-
Polynomial functions can be used as approximations for other elementary functions.
-
To find a polynomial function P that approximates another function f, begin by choosing a number c in the domain of f at which f and P have the same value. That is,
P(c) = f(c)
-
The approximating polynomial is said to be expanded about c or centered at c.
-
Geometrically, P(c) = f(c) means that the graph of P passes through the point (c, f(c)).
-
The goal is to find a polynomial whose graph resembles the graph of f near (c, f(c)).
-
One way to do this is to impose the additional requirement that the slope of the polynomial function be the same as the slope of the graph of f at the point (c, f(c)):
P′(c) = f′(c)
Definitions of nth Taylor Polynomial and nth Maclaurin Polynomial:
If f has n derivatives at c, then the polynomial
P-^n (x) = f(c) + f′(c)(x - c) + (f′′(c)(x - c)^2)/2! + … + (f^(n) (c) (x - c)^n)/n!
is called the nth Taylor polynomial for f at c.
If c = 0, then
P-^n (x) = f(0) + f′(0)(x - c) + (f′′(0)(x - c)^2)/2! + … + (f^(n) (0) (x - c)^n)/n!
is called the nth Maclaurin polynomial for f.
(∞) Σ (n = 0) f^k (0) x^k/k!
-
remainder R-^n (x):
f(x) = P-^n (x) + R-^n (x)
-
f(x) - exact value
-
P-^n (x) - approximate value
-
R-^n (x) - remainder
R-^n (x) = f(x) - P-^n (x)
-
error - the absolute value of R-^n (x):
|R-^n (x)| = |f(x) - P-^n (x)|
Therorem 9.19 - Taylor's Theorem:
If a function f is differentiable through order n + 1 in an interval I containing c, then, for each x in I, there exists a z between x and c such that
f(x) = f(c) + f′(c)(x - c) + (f′′(c)(x - c)^2)/2! + … + (f^(n) (c) (x - c)^n)/n! + R-^n (x)
where
R-^n (x) = f^(n + 1) (z) (x - c)^(n + 1) /(n + 1)!
NOTE: One useful consequence of Taylor's Theorem is that
|R-^n (x)| = max|f^(n + 1) (z)| |x - c|^(n + 1) /(n + 1)!
where max|f^(n + 1) (z)| is the maximum value of f^(n + 1) (z) between x and c. This value is 1 for sine and cosine functions.
Chapter 9.8
Power Series
Definition of Power Series:
If x is a variable, then an infinite series of the form
(∞) Σ (n = 0) a-^n * x^n
= a-^0 + (a-^1 * x) + (a-^2 * x^2) + (a-^3 * x^3) + … + (a-^n * x^n) + …
is called a power series.
More generally, an infinite series of the form
(∞) Σ (n = 0) a-^n * (x - c)^n
= a-^0 + (a-^1 * (x - c)) + (a-^2 * (x - c)^2) + (a-^3 * (x - c)^3) + … + (a-^n * (x - c)^n) + …
is called a power series centered at c, where c is a constant.
NOTE: To simplify the notation for power series, we agree that (x - c)^0 = 1, even if x = c.
Theorem 9.20 - Convergence of a Power Series:
For a power series centered at c, precisely one of the following is true.
1. The series converges only at c.
2. There exists a real number R > 0 such that the series converges absolutely for |x - c| < R, and diverges for |x - c| > R.
3. The series converges absolutely for all x.
-
The number R is the radius of convergence of the power series.
-
If the series converges only at c, the radius of convergence is R = 0.
-
If the series converges for all x, the radius of convergence is R = ∞.
-
If the series converges for a certain interval, the radius of convergence is R.
-
-
The set of all values of x for which the power series converges is the interval of convergence of the power series.
-
The interval of convergence can take any one of the following six forms:
1. Radius: 0
Series converges at: x = c
2. Radius: ∞
Series converges at: (-∞, ∞)
3. Radius: R
Series converges at: (c - R, c + R)
4. Radius: R
Series converges at: (c - R, c + R]
5. Radius: R
Series converges at: [c - R, c + R)
6. Radius: R
Series converges at: [c - R, c + R]
Theorem 9.21 - Properties of Functions Defined by Power Series:
If the function given by
f(x) = (∞) Σ (n = 0) a-^n * (x - c)^n
= a-^0 + (a-^1 * (x - c)) + (a-^2 * (x - c)^2) + (a-^3 * (x - c)^3) + …
has a radius of convergence R > 0, then, on the interval (c - R, c + R), f is differentiable (and therefore continuous). Moreover, the derivative and antiderivative of f are as follows.
1. f′(x) = (∞) Σ (n = 1) na-^n (x - c)^(n - 1)
= a-^1 + 2(x - c) a-^2 + 3(x - c)^2 a-^3 + …
2. ∫ f(x) dx = C + (∞) Σ (n = 0) a-^n (x - c)^(n + 1) /(n + 1)
= C + (a-^0 * (x - c)) + (a-^1 * (x - c)^2 /2) + (a-^2 * (x - c)^3 /3) + …
The radius of convergence of the series obtained by differentiating or integrating a power series is the same as that of the original power series. The interval of convergence, however, may differ as a result of the behavior at the endpoints.
-
Theorem 9.21 states that a function defined by a power series behaves like a polynomial in many ways. It is continuous in its interval of convergence, and both its derivative and antiderivative can be determined by differentiating and integrating each term of the given power series.
Chapter 9.9
Representation of Functions by Power Series
-
You can rewrite a rational function in the form a/(1 - r) to obtain values for a and r to rewrite the function as a geometric power series (∞) Σ (n = 0) ar^n.
Operations with Power Series:
Let f(x) = Σ a-^n x^n and g(x) = Σ b-^n x^n
1. f(kx)
= (∞) Σ (n = 0) a-^n k^n x^n
2. f(x^N)
= (∞) Σ (n = 0) a-^n x^nN
3. f(x) ± g(x)
= (∞) Σ (n = 0) (a-^n ± b-^n) x^n
Chapter 9.10
Taylor and Maclaurin Series
Theorem 9.22 - The Form of a Convergent Power Series:
If f is represented by a power series f(x) = Σ a-^n (x - c)^n for all x in an open interval I containing c,
then a-^n = f^(n) (c) /n! and
f(x) = f(c) + f′(c)(x - c) + (f′′(c)(x - c)^2)/2! + … + (f^(n) (c) (x - c)^n)/n! + …
Definitions of Taylor and Maclaurin Series:
If a function f has derivatives of all orders at x = c, then the series
(∞) Σ (n = 0) (f^(n) (c) (x - c)^n)/n!
= f(c) + f′(c)(x - c) + (f′′(c)(x - c)^2)/2! + … + (f^(n) (c) (x - c)^n)/n! + …
is called the Taylor series for f(x) at c.
Moreover, if c = 0, then the series is the Maclaurin series for f.
Theorem 9.23 - Convergence of Taylor Series:
If lim (-^- (x -> ∞)) R-^n = 0 for all x in the interval I, then the Taylor series for f converges and equals f(x),
f(x) = (∞) Σ (n = 0) (f^(n) (c) (x - c)^n)/n!
Guidelines for Finding a Taylor Series:
1. Differentiate f(x) several times and evaluate each derivative at c.
f(c), f′(c), f′′(c), f′′′(c), … , f^(n) (c), …
Try to recognize a pattern in these numbers.
2. Use the sequence developed in the first step to form the Taylor coefficients f^(n) (c)/n!, annd determine the interval of convergence for the resulting power series
f(c) + f′(c)(x - c) + (f′′(c)(x - c)^2)/2! + … + (f^(n) (c) (x - c)^n)/n! + …
3. Within this interval of convergencce, determine whether or not the series converges to f(x).
Power Series for Elementary Functions:




