
Chapter 7
Applications of Integration
There are many applications of integration. From finding the volume of a solid with a known cross-section to finding the work done by a variable force, integration is as useful as derivatives in the real world, if not more so. Let's begin!
Chapter 7.1
Area of a Region Between Two Curves
Area of a Region Between Two Curves:
If f and g are continuous on [a, b] and g(x) ≤ f(x) for all x in [a, b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is
A = (∫ a->b) [f(x) - g(x)] dx
Steps to Finding the Area of a Region Between Two Curves Without Graphing:
-
Define one function as f and the other as g
-
Algebraically find the points of intersection (if you are not given the domain of the area that you are asked to find)
-
Algebraically test values for both f and g within the interval between the points of intersection (or any given interval)
-
Compare the results from Step 3 to figure out which function is greater within the interval
-
Use the formula above to find the area, making a the lower bound and b the upper bound
Integration as an Accumulation Process:
Representative elements are often taken out of precalculus formulas in the process of creating an integration formula, and an element of change (sometimes Δx) is always present.
Example:
-
known precalculus formula
A = (height)(width)
-
representative element
ΔA = [f(x) - g(x)] dx
-
integration formula
A = (∫ a->b) [f(x) - g(x)] dx
Chapter 7.2
Volume: The Disk Method
-
Solid of revolution - formed when a region in the plane revolves around a line
-
disk - the simplest solid of revolution; formed by revolving a rectangle about an axis adjacent to one side of the rectangle
-

Accumulation Process:
-
known precalculus formula
V = π (R^2) w
-
representative element
ΔV = π [R(x-^i)]^2 Δx
-
integration formula
V = π (∫ a->b) [R(x)]^2 dx
The Disk Method:
To find the volume of a solid of revolution with the disk method, use one of the following:
Horizontal Axis of Revolution:
V = π (∫ a->b) [R(x)]^2 dx
Vertical Axis of Revolution:
V = π (∫ c->d) [R(y)]^2 dy

-
A solid of revolution can have a "hole" in the middle.
-
washer - formed by revolving a rectangle about an axis
-

Washer Method:
Consider a region bounded by an outer radius R(x) and an inner radius r(x)
V = π (∫ a->b) ([R(x)]^2 - [r(x)]^2) dx
-
If you actually think about it, the washer method is only an extension to the disk method. Using rules of integration, the formula for the washer method can be converted into the formula of the outer disk minus the formula of the inner disk (or the hole) using the disk method.
Volumes of Solids with Known Cross Sections:
1. For cross sections of area A(x) taken perpendicular to the x-axis,
V = (∫ a->b) A(x) dx
2. For cross sections of area A(y) taken perpendicular to the y-axis,
V = (∫ c->d) A(y) dy

Here are some visuals to help you get the concept in mind. The base of the solid is the part of it that is touching the ground or the table or whatever, and it is the part that is not one of the cross sections. The cross sections are all of the same shape, some enlarged and some "shrank" down.


To Solve Problems Involving the Volume of a Solid with Known Cross Sections:
-
Figure out the base of the solid, which should be the area under a given function or the area between two given functions (use integration from 7.1)
-
Figure out what geometric shape the cross sections are, and then figure out the formula for the area of the geometric shape
-
Write the formula obtained from Step 2 in terms of the base b (which is both the base of the two-dimensional shape and the base of the three-dimensional solid), this is A(x) or A(y)
-
Plug everything back into the integration formula for solids with known cross sections
-
replace A(x) or A(y) with the formula from Step 3
-
replace b with the formula for the function of the curve or the difference of the two function that borders the area for the base in the problem given
-
-
Integrate and simplify
Chapter 7.3
Volume: The Shell Method
Consider the blue rectangle below, which is spun around an axis of revolution to form the following structure:

-
w - width of the rectangle
-
h - height of the rectangle
-
p - distance between the axis of revolution and the center of the rectangle
When this rectangle is revolved about an axis of revolution, it forms a cylindrical shell of thickness w.
Volume of Shell
= (volume of cylinder) - (volume of hole)
= π (p + w/2)^2 *h) - π (p - w/2)^2 *h)
= 2π phw
ΔV = 2π [p(y) h(y)] Δy
The Shell Method:
To find the volume of a solid of revolution with the shell method, use one of the following:
Horizontal Axis of Revolution:
V = 2π (∫ c->d) [p(y) h(y)] Δy
Vertical Axis of Revolution:
V = 2π (∫ a->b) [p(x) h(x)] Δx

For the disk method, the representative rectangle is always perpendicular to the axis of revolution. However, for the shell method, it is always parallel to the axis of revolution.


Chapter 7.4
Arc Length and Surfaces of Revolution
-
rectifiable curve - arc that has a finite arc length
-
For a function to be rectifiable between (a, f(a)) and (b, f(b)), f ′ has to be continuous on [a, b]. Such a function is continuously differentiable on [a, b], and its graph on the interval [a,b] is a smooth curve.
Definition of Arc Length:
Let the function given by y = f(x) represent a smooth curve on the interval [a, b]. The arc length of f between a and b is
s = (∫ a->b) √(1 + [f′(x)]^2) dx
Similarly, for a smooth curve given by x = g(y), the arc length of g between c and d is
s = (∫ c->d) √(1 + [g′(y)]^2) dy
Definition of Surface of Revolution:
If the graph of a continuous function is revolved about a line the resulting surface is a surface of revolution.
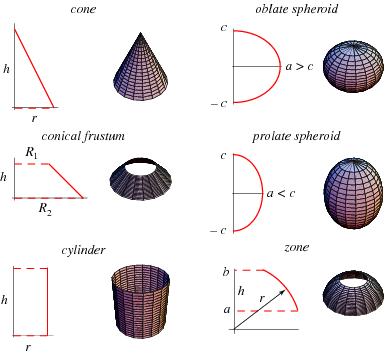
Definition of the Area of a Surface of Revolution:
Let y = f(x) have a continuous derivative on the interval [a, b]. the area S of the surface of revolution formed by revolving the graph of f about a horizontal or vertical axis is
S = 2π (∫ a->b) r(x) √(1 + [f′(x)]^2) dx
where r(x) is the distance between the graph of f and the axis of revolution.
If x = g(y) is on the interval [c, d], the the surface area is
S = 2π (∫ c->d) r(y) √(1 + [g′(y)]^2) dy
where r(y) is the distance between the graph of g and the axis of revolution.
Chapter 7.5
Work
Definition of Work Done by a Constant Force:
If an object is moved a distance D in the direction of an applied force F, then the work W done by the force is defined as
W = FD
Definition of Work Done by a Variable Force:
If an object is moved along a straight line by a continuously varying force F(x), then the work W done by the force as the object is moved from x = a to x = b is
W = lim (-^- (‖Δ‖ -> 0)) [ (n) Σ (i = 1) [Δ W-^i] ]
= (∫ a->b) F(x) dx
1. Hooke's Law: the force F required to compress or stretch a spring (within its elastic limits) is proportional to the distance d that the spring is compressed or stretched from its original length. That is,
F = kd
where the constant of proportionality k (the spring constant) depends on the specific nature of the spring.
2. Newton's Law of Universal Gravitation: the force F of attraction between two particles of masses m-^1 and m-^2 is proportional to the product of the masses and inversely proportional to the square of the distance d between the two particles. That is,
F = k * (m-^1/m-^2)/d^2
If m-^1 and m-^2 are given in grams and d in centimeters, F will be in dynes for a value of k = 6.670*10^-8 cubic centimeters per gram-second squared.
3. Coulomb's Law: the force between two charges q-^1 and q-^2 in a vacuum is proportional to the product of the charges and inversely proportional to the square of the distance d between the two charges. That is,
F = k * (q-^1 * q-^2)/d^2
If q-^1 and q-^2 are given in electrostatic units and d in centimeters, F will be in dynes for a value of k = 1.
-
Work as the summation of increments:
Δ W = (force) (distance increment)
= (F) (Δx)
Δ W = (force increment) (distance)
= (Δ F) (x)
The second interpretation of ΔW is useful in problems involving the movement of nonrigid substances such as fluids and chains.
Here's a handy guide for finding the amount of work done in pumping a fluid:




