Conics | Calculus BC

Chapter 10.1

Conics and Calculus

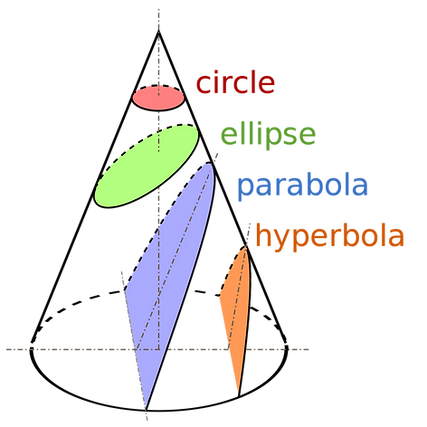
Conics sections, or simply conics, are defined as the intersection of a plane and a double-napped cone. When the plane passes through the vertex, the resulting figure is a degenerative conic.

Conic Sections:

Circle
Parabola
Ellipse
Hyperbola

Degenerative Conics :

Point
Line
Two intersecting lines

General Second-Degree Equation for Conics:

Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0

Conics can be defined as a locus (collection) of points satisfying a certain geometric property.

Circle:

Collection of all points (x, y) that are equidistant from a fixed point (h, k).

Standard Equation:

(x - h)^2 + (y - k)^2 = r^2

Parabola:

Set of all points (x, y) that are equidistant from a fixed line called the directrix and a fixed point called the focus not on the line.

vertex - the midpoint between the focus and the directrix

axis - the line passing through the focus and the vertex

NOTE: A parabola is symmetric with respect to its axis.

Theorem 10.1 - Standard Equation of a Parabola:

The standard form of the equation of a parabola with vertex (h, k) and directrix y = k - p is

(x - h)^2 = 4p (y - k)

(vertical axis)

For directrix x = h - p, the equation is

(y - k)^2 = 4p (x - h)

(horizontal axis)

The focus lies on the axis p units (directed distance) from the vertex. The coordinates of the focus are as follows.

(h, k + p)

(vertical axis)

(h + p, k)

(horizontal axis)

focal chord - a line segment that passes through the focus of a parabola and has endpoints on the parabola

latus rectum - the specific focal chord perpendicular to the axis of the parabola

In physics, a surface is called reflective if the tangent line at any point on the surface makes equal angles with an incoming ray and the resulting outgoing ray.

angle of incidence - the angle corresponding to the incoming ray

angle of reflection - the angle corresponding to the outgoing ray

Another type of reflective surface is that formed by revolving a parabola about its axis. A special property of parabolic reflectors is that they allow us to direct all incoming rays parallel to the axis through the focus of the parabola — this is the principle behind the parabolic mirrors used in reflecting telescopes. Conversely, all light rays emanating from the focus of a parabolic reflector used in a flashlight are parallel.

Theorem 10.2 - Reflective Property of a Parabola:

Let P be a point on a parabola. The tangent line to the parabola at the point P makes equal angles with the following two lines

The line passing through P and the focus
The line passing through P parallel to the axis of the parabola

Ellipse:

Set of all points (x, y) the sum of whose distances from two distinct fixed points called foci is constant. The line through the foci intersects the ellipse at two points, called the vertices.

major axis - the chord joining the vertices; its midpoint is the center of the ellipse

minor axis - the chord perpendicular to the major axis at the center

Theorem 10.3 - Standard Equation of an Ellipse:

The standard form of the equation of an ellipse with center (h, k) and major and minor axes of lengths 2a and 2b, where a > b, is

(x - h)^2 /a^2 + (y - k)^2 /b^2 = 1

(major axis is horizontal)

(x - h)^2 /b^2 + (y - k)^2 /a^2 = 1

(major axis is vertical)

The foci lie on the major axis, c units from the center, with c^2 = a^2 - b^2.

NOTE: You can imagine the definition of an ellipse by imagining two thumbtacks placed at the foci. If the ends of a fixed length of a string are fastened to the thumbtacks and the string is drawn taut with a pencil, the path traced by the pencil will be an ellipse.

Theorem 10.4 - Reflective Property of an Ellipse:

Let P be a point on an ellipse. The tangent line at point P makes equal angles with the lines through P and the foci.

Definition of Eccentricity of an Ellipse:

The eccentricity e of an ellipse is given by the ratio

e = c / a

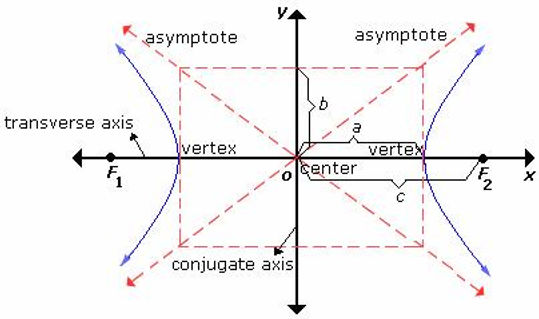
Hyperbola:

Set of all points (x, y) for which the absolute value of the difference between the distances from two distinctly fixed points called foci is constant. The line through the two foci intersects a hyperbola at two points called the vertices.

transverse axis - the line segment connecting the vertices

center - the midpoint of the transverse axis

One distinguishing feature of a hyperbola is that its graph has two separate branches.

Theorem 10.5 - Standard Equation of a Hyperbola:

The standard equation of a hyperbola with center (h, k) is

(x - h)^2 /a^2 - (y - k)^2 /b^2 =1

(transverse axis is horizontal)

(y - k)^2 /a^2 - (x - h)^2 /b^2 = 1

(transverse axis is vertical)

The vertices are a units from the center, and the foci are c units from the center, where, c^2 = a^2 + b^2.

NOTE: The constants a, b, and c do not have the same relationship for hyperbolas as they do for ellipses. For hyperbolas, c^2 = a^2 + b^2, but for ellipses, c^2 = a^2 - b^2.

An important aid in sketching the graph of a hyperbola is the determination of its asymptotes. Each hyperbola has two asymptotes that intersect at the center of the hyperbola. The asymptotes pass through the vertices of a rectangle of dimensions 2a by 2b, with its center at (h, k). The line segment of length 2b joining (h, k + b) and (h, k - b) is referred to as the conjugate axis of the hyperbola.

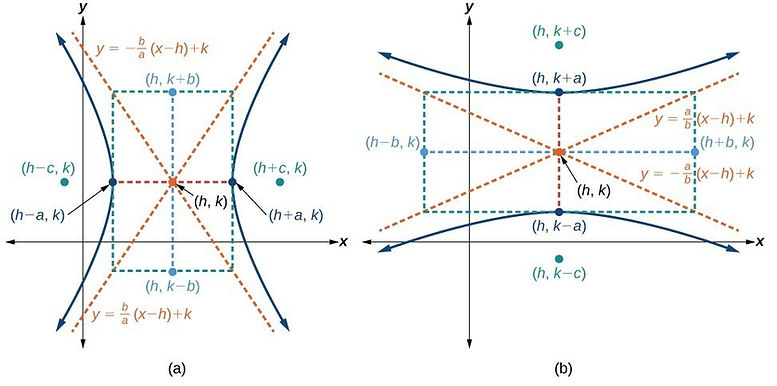
Theorem 10.6 - Asymptotes of a Hyperbola:

For a horizontal transverse axis, the equations of the asymptotes are

y = k + (b/a) (x - h)

and

y = k - (b/a) (x - h)

For a verticle transverse axis, the equations of he asymptotes are

y = k + (a/b) (x - h)

and

y = k - (a/b) (x - h)

Definition of Eccentricity of a hyperbola :

The eccentricity of a hyperbola is given by the ratio

e= c / a

Because c > a for hyperbolas, it follows that e > 1 for hyperbolas. If the eccentricity is large, the branches of the hyperbola are nearly flat. If the eccentricity is close to 1, the branches of the hyperbola are more pointed.