Applications of Differentiation

Chapter 3

After learning how to differentiate, it is important to know what differentiation can be used for. Differentiation has many applications, and here we will investigate a few of them.

I hope this playlist helps with your concentration. 😁

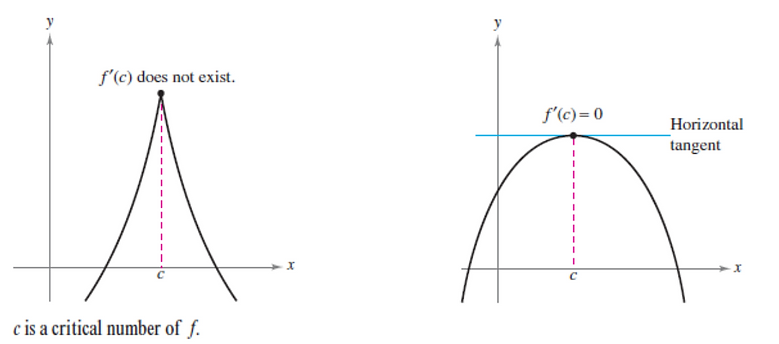
Chapter 3.1

Extrema on an Interval

Definition of Extrema:

Let f be defined on an interval I containing c.

f(c) is the minimum of f on I if f(c) ≤ f(x) for all x in I.
f(c) is the maximum of f on I if f(c) ≥ f(x) for all x in I.

The minimum and maximum of a function on an interval are the extreme values, or extrema (singular, extremum), of the function in the interval.

The minimum and maximum of a function on an interval are also called the absolute minimum and absolute maximum on the interval.

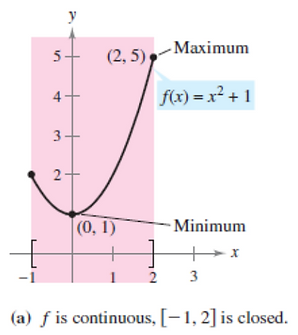
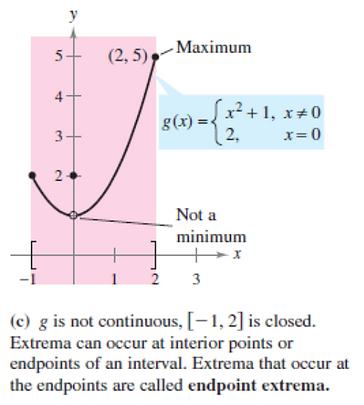
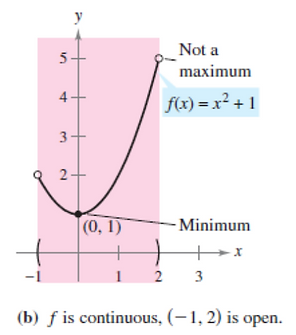
Theorem 3.1 - The Extreme Value Theorem:

If f is continuous on a closed interval [a, b], then f has both a minimum and a maximum on the interval.

Definition of Relative Extrema:

If there is an open interval containing c on which f(c) is a maximum, then f(c) is called a relative maximum of f, or you can say that f has a relative maximum at (c, f(c)).
If there is an open interval containing c on which f(c) is a minimum, then f(c) is called a relative minimum of f, or you can say that f has a relative minimum at (c, f(c)).

NOTE: The plural of maximum is maxima, and the plural of minimum is minima.

Definition of a Critical Number:

Let f be defined at c. If f′(c) = 0 or if f is not differentiable at c, then c is a critical number of f.

Theorem 3.2 - Relative Extrema Occur only at Critical Numbers:

If f has a relative minimum or relative maximum at x = c, then c is a critical number of f.

Guidelines for Finding Extrema on a Closed Interval:

To find the extrema of a continuous function f on a closed interval [a, b]:

Find the critical number of f in (a, b)
Evaluate f at each critical number in (a, b)
Evaluate f at each endpoint of [a, b]
The least of these values is the minimum. The greatest is the maximum.

In Other Words:

Find the derivative of f
Set f′ to 0 and solve the equation for x
Plug the obtained value(s) of x back into f(x) -- this gives you the extremum/extrema of f
Solve for f(a) and f(b)
Out of the critical number(s) found, f(a), and f(b) -- the smallest value is the minimum and the largest value is the maximum

Chapter 3.2

Rolle's Theorem and the Mean Value Theorem

Theorem 3.3 - Rolle's Theorem:

Let f be continuous on the closed interval [a, b] and differentiable on the open interval (a, b).

If f(a) = f(b), then there is at least one number c in (a, b) such that f′(c) = 0.

NOTE: Rolle's Theorem guarantees at least one x-value in (a, b) for which the graph of f has a horizontal tangent. If the differentiation requirement is dropped, there will still be a critical number within the interval, but it may not yield a horizontal tangent. (You have a sharp point here!)

Theorem 3.4 - The Mean Value Theorem:

If f is continuous on the closed interval [a, b] and is differentiable on the open interval (a, b), then there exists a number c in (a, b) such that

f′(c) = (f(b) - f(a)) / (b - a)

Alternative Form:

f(b) = f(a) + (b - a) f′(c)

Reference Videos:

Rolle's Theorem

The Mean Value Theorem

Chapter 3.3

Increasing & Decreasing Functions and the First Derivative Test

Definition of Increasing and Decreasing Functions:

A function f is increasing on an interval if:

for any two numbers x-^1 and x-^2 in the interval,

x-^1 < x-^2 implies f(x-^1) < f(x-^2).

A function f is decreasing on an interval if:

for any two numbers x-^1 and x-^2 in the interval,

x-^1 < x-^2 implies f(x-^1) > f(x-^2).

Theorem 3.5 - Test for Increasing and Decreasing Functions:

Let f be a function that is continuous on the closed interval [a, b] and differentiable on the open interval (a, b).

If f′(x) > 0 for all x in (a, b), then f is increasing on [a, b].
If f′(x) < 0 for all x in (a, b), then f is decreasing on [a, b].
If f′(x) = 0 for all x in (a, b), then f is constant on [a, b].

In Other Words:

Positive derivative — function is increasing
Negative derivative — function is decreasing
Zero as a derivative — function is constant

Guidelines for Finding Intervals on Which a Function Is Increasing or Decreasing:

Let f be continuous on the interval (a, b).

To find the open intervals on which f is increasing or decreasing:

Locate the critical number of f in (a, b), and use these numbers to determine test intervals.
Determine the sign of f′ (x) at one value in each of the intervals.
Use Theorem 3.5 to determine whether f is increasing or decreasing in each interval.

These guidelines are also valid if the interval (a, b) is replaced by an interval of the following forms:

(-∞, b)

(a, ∞)

(-∞, ∞)

Theorem 3.6 - The First Derivative Test:

Let c be a critical number of a function f that is continuous on an open interval I containing c.

If f is differentiable on the interval except possibly at c, then f(c) can be classified as follows:

If f′(x) changes from negative to positive at c, then f has a relative minimum at (c, f(c)).
If f′(x) changes from positive to negative at c, then f has a relative maximum at (c, f(c)).
If f′(x) is positive (or negative) on both sides of c, then f(c) is neither a relative minimum nor a relative maximum.

Chapter 3.4

Concavity and the Second Derivative Test

Definition of Concavity:

Let f be differentiable on an open interval I.

The graph of f is concave upwards on I if f′ is increasing on the interval.
The graph of f is concave downwards on I if f′ is decreasing on the interval.

Graphical Interpretation:

Let f be differentiable on I.

Concave Upwards - graph of f lies above all tangent lines
Concave Downwards - graph of f lies below all tangent lines

Theorem 3.7 - Test for Concavity:

Let f be a function whose second derivative exists on an open interval I.

If f′′(x) > 0 for all x in I, then the graph of f is concave upwards in I.
If f′′(x) < 0 for all x in I, then the graph of f is concave downwards in I.

To apply Theorem 3.7, locate the x-values at which f′′(x) = 0 or f′′ does not exist. Second, use these x-values to determine test intervals. Finally, test the sign of f′′(x) in each of the test intervals.

Definition of Point Inflection:

Let f be a function that is continuous on an open interval and let c be a point in the interval.

If the graph of f has a tangent line at (c, f(c)),

then this point is a point of inflection of the graph of f

if the concavity of f changes from upward to downward (or downward to upward) at the point.

NOTE: This definition requires that the tangent line exists at the point of inflection.

Theorem 3.8 - Points of Inflection:

If (c, f(c)) is a point of inflection of the graph of f,

then either f′′(c) = 0 or f′′ does not exist at x = c.

NOTE: The converse is not always true.

Theorem 3.9 - Second Derivative Test:

Let f be a function such that f′(c) = 0 and the second derivative of f exists on an open interval containing c.

If f′′(c) > 0, then f has a relative minimum at (c, f(c))
If f′′(c) < 0, then f has a relative maximum at (c, f(c))
If f′′(c) = 0, the test fails. (f may have a relative maximum, a relative minimum, or neither. In such cases, the First Derivative Test can be used.)

Chapter 3.5

Limits at Infinity

Limits at Infinity: the value that f(x) approaches as x increases or decreases without bound.

Definition of Limits at Infinity:

Let L be a real number.

1. The statement lim (-^- (x -> ∞)) f(x) = L mean:

for each 𝈡 > 0

there exists an M > 0

such that |f(x) - L| < 𝈡

whenever x > M.

(f(x) is within 𝈡 units of L as x -> ∞)

2. The statement lim (-^- (x -> -∞)) f(x) = L means:

for each 𝈡 > 0

there exists an N < 0

such that |f(x) - L| < 𝈡

whenever x < N.

Definition of Horizontal Asymptote:

The line y = L is a horizontal asymptote of the graph of f if

lim (-^- (x -> ∞)) f(x) = L

or if

lim (-^- (x -> -∞)) f(x) = L

Theorem 3.10 - Limits at Infinity:

If r is a positive rational number and c is any real number, then

lim (-^- (x -> ∞)) (c /x^r) = 0

Furthermore, if x^r is defined when x < 0, then

lim (-^- (x -> -∞)) (c /x^r) = 0

Indeterminate Form: ∞/∞

Finding Limits at ±∞ of Rational Functions:

BOBO BOTN EATS DC

BOBO - If the degree is bigger on bottom, then y = 0

BOTN - If the degree is bigger on top, then there is no limit (in other words, the limit does not exist)

EATS DC - If the exponents are the same, divide coefficients.

Definition of Infinite Limits at Infinity:

Let f be a function defined on the interval (a, ∞)

1. The statement lim (-^- (x -> ∞)) f(x) = ∞ means:

for each positive number M,

there is a corresponding number N > 0

such that f(x) > M whenever x > N.

2. The statement lim (-^- (x -> ∞)) f(x) = -∞ means:

for each negative number M,

there is a corresponding number N > 0

such that f(x) < M whenever x > N

A Tip for Finding the Limit for Rational Functions with 2 Horizontal Asymptotes:

- Divide both the numerator and the denominator by the variable used raised to the highest power present in the entire rational function.

- When radicals are present,

write x as √(x^2) for x > 0

write x as -√(x^2) for x < 0

- Take the limit.

Chapter 3.6

A Summary of Curve Sketching

Guidelines for Analyzing the Graph of a Function:

Determine the domain and the range of the function.
Determine the intercepts, asymptotes, and symmetry of the graph.
Locate the x-values for which f′(x) and f′′(x) either are zero or do not exist. Use the results to determine relative extrema and points of inflection.

Chapter 3.7

Optimation Problems

Guidelines for Solving Applied Minimum and Maximum Problems:

Identify all given quantities and quantities to be determined. If possible, make a sketch.
Write a primary equation for the quantity that is to be maximized or minimized.
Reduce the primary equation to one having a single independent variable. This may involve the use of secondary equations relating the independent variables of the primary equation.
Determine feasible domains of the primary equation. That is, determined the values for which the stated problem makes sense.
Determine the desired maximum or minimum value using calculus techniques.

Chapter 3.8

Newton's Method

Newton's Method for Approximating the Zeros of a Function:

Let f(c) = 0, where f is differentiable on an open interval containing c. To approximate c:

1. Make an initial estimate x, that is close to c (a graph is helpful)

2. Determine a new approximation

x-^(n + 1)

= x-^n - ((f(x-^n)) / (f′(x-^n)))

3. If |x-^(n) - x-^(n + 1)| is within the desired accuracy, let x^(n + 1) serve as the final approximation. Otherwise, return to Step 2 and calculate a new approximation.

Each successive application of this procedure is called an iteration.

When the approximations approach a limit, the sequence x-^1, x-^2, x-^3, …, x-^n, … is said to converge.
If the limit is c, it can be shown that c must be a zero of f.
Since Newton's Method involves division by f′(x-^n), it will fail if the derivative is 0 for any x-^n in the sequence.
This problem can usually be overcome by choosing a different value for x-^1.

Condition for Convergence:

|(f(x) f′′(x)) / [f′(x)]^2| < 1

Solution by Radicals - when the exact solution is written in terms of square roots and cube roots.

Chapter 3.9

Differentials

Tangent Line Approximation (or Linear Approximation) of f at c:

Let f be a function differentiable at c. The tangent approximation or linear approximation of f at c is the equation for the tangent line at the point (c, f(c)):

y - f(c) = f′(c) (x - c)

y = f(c) + f′(c) (x - c)

y is a linear function of x because c is constant.
The values of y can be used as approximations (to any desired accuracy) to the values of f by restricting the values of x to be sufficiently close to c.
In other words, as x approaches c, the limit of y is f(c).

Definition of Differentials:

Let y = f(x) represent a function that is differentiable on an open interval containing x. The differential of x is any nonzero real number. The differential of y is:

dy = f′(x) dx

Differential of x — dx = Δx
Differential of y — dy ≈ Δy

Error Propagation:

If:

x => measured value

x + Δx => exact value

Then:

Δx => error in measurement

If the measured value x is used to compute another value f(x), the difference between f(x + Δx) and f(x) is the propagated error.

f(x + Δx) - f(x) = Δy

Δy => propagated error

Related error - ratio between the differential of the variable and the variable itself

Examples: dx/x, dv/v, etc.

Percent error -percentage obtained from solving for the relative error

Calculating Differentials:

Differentiation rules can be written in differential form.

Example:

u and v are differentiable functions of x.

The definition of differentials gives us:

du = u′ dx and dv = v′ dx

So, to write the differential form of the Product Rule:

d [uv] = d/dx [uv] dx

= [uv′ + vu′] dx

= uv′ dx + vu′ dx

= u dv + v du

Differential Formulas:

Let u and v be differentiable functions of x.

Constant Multiple:

d [cu] = c du

Sum or Difference:

d [u ± v] = du ± dv

Product:

d [uv] = u dv + v du

Quotient:

d [u / v] = (v du - u dv) / v^2

TIP: Take the differentiation rule and replace u′ with du and v′ with dv.

Leibniz Notation - provides easy way to remember several important calculus formulas by making it seem as though the formulas were derived from algebraic manipulations of differentials

Example: dy / dx

Lagrange Notation - uses the prime symbol " ′ " and is the most commonly used when dealing with functions of a single variable. Handy in long calculations because of its simplicity

Examples: f′, y′, etc.

Differentials can be used to approximate function values. To do this for the function given by y = f(x), use the following formula:

f(x + Δx) ≈ f(x) + dy = f(x) + f′(x) dx

(This formula is derived from the approximation Δy = f(x + Δx) - f(x) ≈ dy)

The key to using this formula is to choose a value for x that makes the calculations easier.