Finding Derivatives | Differentiation

As x approaches c, the secant line approaches the tangent line.

If a function is not continuous at x = c, it is also not differentiable at x = c.

Theorem 2.1 - Differentiability Implies Continuity:

If f is differentiable at x = c, then f is continuous at x = c.

NOTE: THE CONVERSE IS NOT TRUE!!!

It is possible for a function to be continuous but not differentiable at x = c. Continuity does not imply differentiability.

Chapter 2.3

Product and Quotient Rules and Higher-Order Derivatives

Theorem 2.7 - The Product Rule:

The product of two differentiable functions f and g is itself differentiable. Moreover, the derivative of fg is the first function time the derivative of the second, plus the second function times the derivative of the first.

d/dx [f(x) g(x)]

= f(x) g′(x) + g(x) f′(x)

The product rule can be extended to cover products involving more than two factors.

EX:

d/dx [f(x) g(x) h(x)]

= f′(x) g(x) h(x) + f(x) g′(x) h(x) + f(x) g(x) h′(x)

Theorem 2.8 - The Quotient Rule:

The quotient f/g of two differentiable functions f and g is itself differentiable at all values of x for which g(x) ≠ 0. Moreover, the derivative of f/g is given by:

d/dx [f(x)/g(x)]

= (g(x) f′(x) - f(x) g′(x))/([g(x)]^2)

Theorem 2.9 - Derivatives of Trigonometric Functions:

d/dx [tan x] = sec^2 x

d/dx [sec x] = sec x tan x

d/dx [cot x] = -csc^2 x

d/dx [csc x] = -csc x cot x

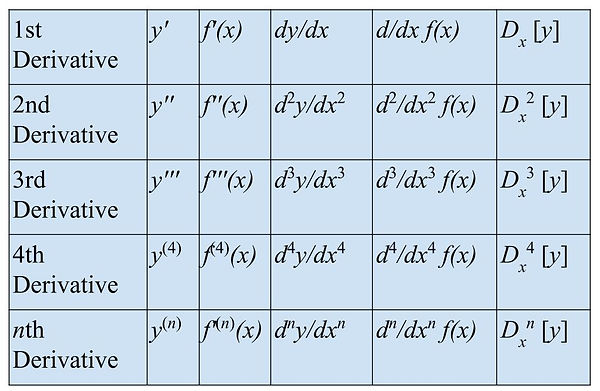
Higher-Order Derivatives:

You can define derivatives of any positive integer order .

You can obtain an acceleration function by differentiating a velocity function:

Position Function:

s(t)

Velocity Function:

v(t) = s′(t)

Acceleration Function:

a(t) = v′(t) = s′′(t)

Chapter 2.2

Basic Differentiation Rules and Rates of Change

Theorem 2.2 - The Constant Rule:

The derivative of a constant function is 0.

d/dx [c] = 0

c is a real number.

Theorem 2.3 - The Power Rule:

If n is a rational number, then the function f(x) = x^n is differentiable and

d/dx [x^n] = nx^(n - 1)

For f to be differentiable at x = 0, n must be a number such that x^(n - 1) is defined on an interval containing 0.

Power Rule When n = 1:

d/dx [x] = 1

Theorem 2.4 - The Constant Multiple Rule:

If f is a differentiable function and c is a real number, then cf is also differentiable and

d/dx [c f(x)] = cf′(x)

Informally, the Constant Multiple states that constants can be factored out of the differentiation process, even if constants appear in the denominator (you factor out 1/(a number)).

Power Rule = Constant Multiple Rule:

d/dx [cx^n] = cnx^(n - 1)

Theorem 2.5 - The Sum and Difference Rules:

The sum/difference of two differentiable functions f and g is itself differentiable. Moreover, the derivative of f + g / f - g is the sum/difference of the derivatives of f and g.

The Sum Rule:

d/dx [f(x) + g(x)] = f′(x) + g′(x)

The Difference Rule:

d/dx [f(x) + g(x)] = f′(x) + g′(x)

Theorem 2.6 - The Derivatives of Sine and Cosine Functions:

d/dx [sin x] = cos x

d/dx [cos x] = -sin x

Position Function:

Function s that gives the position (relative to the origin) of an object as a function of time t.

Δs = s(t + Δt) - s(t)

Average Velocity:

Change in Distance/Change in Time

= Δs/Δt

Instantaneous Velocity at Time t:

v(t)

= lim (-^- (Δt -> 0)) ((s(t + Δt) - s(t)) / Δt)

= s′(t)

Speed - absolute value of velocity; cannot be negative

Free-Falling Objects with Gravity:

s(t) = 0.5(gt^2) + v-^0(t) + s-^0

g is the acceleration due to gravity:

-32ft/sec^2 or -9.8m/sec^2 on Earth

v-^0 is the initial velocity

s-^0 is the initial height

Chapter 2.1

The Derivative and the Tangent Line Problem

The Tangent Line Problem:

Given: Function f and a point P on the function.

Goal: To find the equation of the tangent line to f at P. (A tangent line is a line that touches the graph of a function at only one point without crossing the graph of the function.)

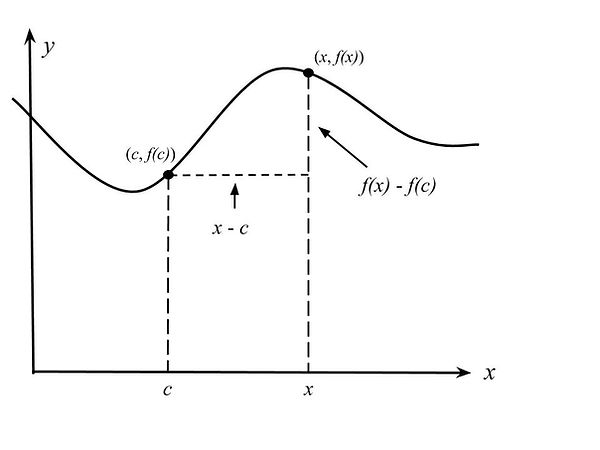
To solve the tangent line problem, start by finding the slope of the tangent line at point P. To do so, we find the limit of the secant lines through the function at point P. (A secant line is just any line that intersects the graph of the function at more than one point. As the two points that the secant line is crossing gets closer and closer together, we are zooming in on the tangent line of the function, or the limit of the secant lines.)

To find the limit, we use the slope of the secant line crossing through P and a second point on f.

Here's how to label the points:

P: (c, f(c))

A second point: (c + Δx, f(c + Δ x))

Δx stands for the change in x as we go from point P to the second point where the secant line intersects the graph of the function.

The slope of the secant line is:

m(-^sec) = (f(c + Δx) - f(c)) / ((c + Δ x) - c)

= (f(c + Δx) - f(c)) / Δ x

You can obtain more accurate approximations of the slope of the tangent line by choosing points closer to the point of tangency. Thus the limit of the slope of the secant line is the slope of the tangent line.

Definition of Tangent Line with Slope m:

If f is defined on an open interval containing c, and if the limit

lim (-^- (Δx -> 0)) (Δy / Δx)

= lim (-^- (Δx -> 0)) ((f(c + Δx) - f(c)) / Δx)

= m

exists, then the line passing through (c, f(c)) with slope m is the tangent line to the graph of f at the point (c, f(c)).

NOTE: m here is also called the slope of the graph of f at x = c.

Vertical Tangent Line:

If f is continuous at c and

lim (-^- (Δx -> 0)) ((f(c + Δx) - f(c)) / Δx)

= ∞ or -∞

the vertical line x = c passing through (c, f(c)) is a vertical tangent line to the graph of f.

Differentiation - the process of finding the derivative of a function

Definition of the Derivative of a Function:

The derivative of f at x is given by

f′(x) = lim (-^- (Δx -> 0)) ((f(x + Δx) - f(x)) / Δx)

provided the limit exists. For all x for which this limit exists, f′ is a function of x.

A function is differentiable at x if its derivative exists at x and is differentiable on an open interval (a, b) if it is differentiable at every point on the interval.

Notations for Derivatives:

f′(x)
dy/dx - read as "the derivative of y with respect to x"
y′ - read as "y prime"
d/dx [f(x)]
D (-^ x) [y]

Alternative Form of Derivative:

f′(c) = lim (-^- (Δx -> c)) ((f(x) - f(c)) / (x - c))

exists if given the following one-sided limits exist and are equal

lim (-^- (Δx -> c-)) ((f(x) - f(c)) / (x - c))

-- Derivative from the left

lim (-^- (Δx -> c+)) ((f(x) - f(c)) / (x - c))

-- Derivative fromthe right

NOTE: f is differentiable on the open interval [a, b] if it is differentiable on (a, b) and if the derivative from the right at a and the derivative from the left at b both exist.

Chapter 2 and Chapter 5.1A and 5.4A

Differentiation

Derivatives might sound like something out of another world, but with practice, they are not that hard to find!

I hope the music helps! 😆

Chapter 2.4

The Chain Rule

Theorem 2.10 - The Chain Rule:

If y = f(u) is a differentiable function of u and u = g(x) is a differentiable function of x, then y = f(g(x)) is a differentiable function of x and

dy/dx = (dy/du) * (du/dx)

or, equivalently:

d/dx [f(g(x))] = f′(g(x)) g′(x)

When applying the Chain Rule, it is helpful to think of the composite function f ∘ g as having two parts -- an inner part and an outer part.

y = f(g(x)) = f(u) ,

so y′ = f′(u) * u′

Here, g or u is the inner function, and f is the outer function.

Theorem 2.11 - The General Power Rule:

If y = [u(x)]^n, where u is a differentiable function of x and n is a rational number, then

dy/dx = n[u(x)]^(n - 1) * du/dx

or, equivalently:

d/dx [u^n] = nu^(n - 1) * u′

Chain Rule Versions of Trig Function Derivatives:

d/dx [sin u] = (cos u) u′

d/dx [tan u] = (sec^2 u) u′

d/dx [sec u] = (sec u tan u) u′

d/dx [cos u] = - (sin u) u′

d/dx [cot u] = - (csc^2 u) u′

d/dx [csc u] = - (csc u cot u) u′

Chapter 2.5

Implicit Differentiation

Explicit Form:

y = 3x^2 - 5

y is explicitly written as a function of x.

Implicit Form:

2x^2 + xy + y^2 = 0

The function is only implied by an equation. (Implt, implicit... get it?)

Guidelines for Implicit Differentiation:

Differentiate both sides of the equation with respect to x, using the Chain Rule for terms with y.
Collect all terms involving dy/dx on one side of the equation and move everything else to the other side.
Factor dy/dx out of its side of the equation.
Solve for dy/dx.

Chain Rule Involving y:

(I organized this equation myself 😉)

d/dx [y^n] = ny^(n - 1) * dy/dx

d/dx [(y and whatever-numbers-and-other-stuff-stuck-to-it) ^n]

= n(y and whatever-numbers-and-other-stuff-stuck-to-it) ^(n - 1) * dy/dx

I hope this helps! 😄

Chapter 5.1A

Differentiation of the Natural Logarithmic Function

Theorem 5.3 - Derivative of the Natural Logarithmic Function:

Let u be a differentiable function of x .

1. d/dx [ln x] = 1/x , x > 0

2. d/dx [ln u] = (1/u) * (du/dx)

= u′/u , u > 0

Theorem 5.4 - Derivative Involving Absolute Value:

If u is a differentiable function of x such that u ≠ 0, then

d/dx [ln |u|] = u′/u

A New Way of Finding the Derivative (When You Have y = ... :

Take the ln of both sides of the original equation
Find the derivative of both sides (ln y = y′/y)
Multiply both sides with y after you find the derivative of the side of the equation without y
Substitute y with the other half of the original equation
Simplify

Chapter 5.4A

Differentiation of the Natural Exponential Function

Theorem 5.11 - Derivatives of the Natural Exponential Function:

Let u be a differentiable function of x.

d/dx [e^x] = e^x

d/dx [e^u] = e^u * (du/dx)

(The second equation is actually nothing new -- just the first equation along with the Chain Rule reapplied. 😉 )

ln versus e

Comparing the Natural Logarithmic Function with the Natural Exponetial Function

What is the Natural Logarithmic Function?

It is a log function with base e, and it is written as ln.

Theorem 5.1 - Properties of the Natural Logarithmic Function:

Domain: (0, ∞)
Range (-∞, ∞)
Continuous
Increasing
One to one
Concave downward

Theorem 5.2 - Logarithmic Properties:

If a and b are positive numbers and n is rational, then the following properties are true:

ln(1) = 0

ln (ab) = ln a + ln b

ln (a/b) = ln a - ln b

ln (a^n) = n ln a

Definition of the Natural Exponential Function:

The natural exponential function is the inverse function of the natural logarithmic function f(x) = ln x is called the natural exponential function and is denoted by

f^(-1) (x) = e^x

That is,

y = e^x if and only if x = ln y

Properties of the Natural Exponential Function:

Domain: (-∞, ∞)
Range: (0, ∞)
Continuous
Increasing
One to one
Concave upward
lim (-^- x -> -∞) (e^x) = 0
lim(-^- x -> ∞) (e^x) = ∞

Theorem 5.10 - Operations with Exponential Functions :

(e^a)*(e^b) = e^(a + b)

(e^a)/(e^b) = e^(a - b)

Inverse Relationships:

ln (e^x) = x

e^(ln x) = x

Chapter 2.6