Antiderivatives and Integrals | Integration

Chapter 4 and Chapter 5

Antiderivatives and Integration

What's the opposite of a derivative? Well, it is an antiderivative. No, this is not a joke, antiderivatives are a thing. In this section, we will take a look at antiderivatives and the process known as integration — which is exactly the opposite of differentiation. So let's get started!

I hope the music helps! 😉😁

Chapter 4.1

Antiderivatives and Indefinite Integration

Definition of Antiderivative:

A function F is an antiderivative of f on an interval I if F'(x) = f(x) for all x in I.

Theorem 4.1 - Representation of Antiderivatives:

If F is an antiderivative of f on an interval I, then G is an antiderivative of f on the interval I if and only if G is of the form G(x) = F(x) + C, for all x in I where C is a constant.

This means that you can add any constant C to an antiderivative of a function and get another function, which is another the antiderivative of the first function. A function can have many different antiderivatives — and the only difference between them is an added constant.

constant of integration - the constant C

general antiderivative of f - the family of functions represented by G

differential equation in x and y - an equation that involves x, y, and derivatives of y

Example: y′ = 2x + 1

G(x) = x^2 + C is the general solution of the differential equation G′(x) = 2x

Notation for Antiderivatives:

y = ∫ f(x) dx = F(x) + C

integrand - the function to be integrated - f(x)

variable of integration - the variable being integrated - x

constant of integration - the constant C

Antidifferentiation and Indefinite Integration:

different names for the same thing.
the operation of finding all solutions of dy = f(x) dx
denoted by an integral sign: ∫
general solution:

y = ∫ f(x) dx = F(x) + C

∫ f(x) dx is read as the antiderivative of f with respect to x
the differential dx serves to identify x as the variable of integration
indefinite integral and antiderivative are synonyms of each other, and they both represent the solution to an integration or an antidifferentiation problem

Differentiation and Integration are Inverses:

∫ F′(x) dx = F(x) + C

d/dx [ ∫ f(x) dx ] = f(x)

Basic Integration Rules:

general solution - includes the constant of integration, C

Example: F(x) = x^3 +2x + C

initial condition - the value of y = F(x) for one value of x

Example: F(2) = 4

particular solution - when C is replaced by an actual number

Example: F(x) = x^3 +2x + 8

Just in case if you wondering how dx worked its way into y = ∫ f(x) dx, consider this:

When solving a differentiable equation dy/dx = f(x), it is often convenient to write it in the equivalent differential form dy = f(x) dx

And when you put that second equation under the integral sign, you end up with the dx inside of the y = ∫ f(x) dx

Chapter 4.2

Area of a Region

Sigma Notation:

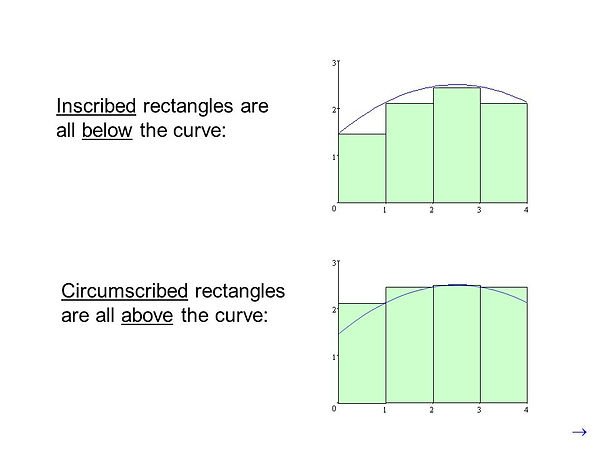
When approximating an area under a curve:

f(m-^i) Δx ≤ f(M-^i) Δx

(area of inscribed rectangle ≤ area of circumscribed rectangle)

f(m-^i) = minimum value of f(x) in the ith subinterval
f(M-^i) = maximum value of f(x) in the ith subinterval

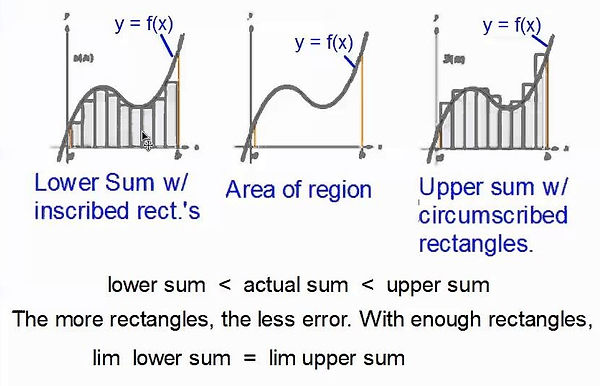
s(n) < A(n) < S(n)

s(n) = (n) Σ (i = 1) [ f(m-^i)Δx] = area of inscribed rectangles = lower sum
S(n) = (n) Σ (i = 1) [ f(M-^i)Δx] = area of circumscribed rectangles = upper sum

(The n should go above the Σ and the i = 1 should go below Σ. I'm sorry but this text field does not let me type the expression in the way that it is supposed to look like.)

The interval [a, b] is divided into n subintervals, each of width Δx = (b - a)/n

Theorem 4.3 - Limits of the Lower and Upper Sums:

Let f be continuous and nonnegative on the interval [a, b]. The limits as n -> ∞ of both the lower and upper sums exist and are equal to each other. That is,

lim (-^- (x -> ∞)) s(n)

= lim (-^- (x -> ∞)) [ (n) Σ (i = 1) [ f(m-^i)Δx] ]

= lim (-^- (x -> ∞)) [ (n) Σ (i = 1) [ f(M-^i)Δx] ]

= lim (-^- (x -> ∞)) S(n)

Where

Δx = (b - a)/n
f(m-^i) is the minimum value of f on the subinterval
f(M-^i) is the maximum value of f on the subinterval

Definition of the Area of a Region in the Plane:

Let f be continuous and nonnegative on the interval [a, b]. The area of the region bounded by the graph of f, the x-axis, and the verticle lines x = a and x = b is the following:

Area = lim (-^- (x -> ∞)) [ (n) Σ (i = 1) [ f(c-^i)Δx] ],

x-^(i - 1) ≤ c ≤ x-^i

Where:

Δx = (b - a)/n
c-^i = a + iΔx when calculating from the right
c-^i = a + (i - 1) Δx when calculating from the left

I have a shortened version of this definition:

Calculating from the right:

Σ f(a + ((b - a)/n)i) * ((b - a)/n)

Calculating from the left:

Σ f(a + ((b - a)/n)*(i - 1)) * ((b - a)/n)

NOTE: The upper and lower bounds must be constant with respect to the index of summation.

Theorem 4.2 - Summation Formulas:

Chapter 4.3

Riemann Sums and Definite Integrals

In the previous section, the definition of area included the use of subintervals of equal width. This was for computational convenience only, for subintervals of equal width are not actually necessary when finding such an area.

partition of an interval - a division of an interval into several disjoint sub-intervals
disjoint - having no elements in common

Definition of a Riemann Sum:

Let f be defined on the closed interval [a, b], and let Δ be a partition of [a, b] given by

a = x-^0

b = x-^n

x-^0 < x-^1 < x-^2 < ... < x-^(n - 1) < x-^n

Where Δx-^i is the width of the ith subinterval.

If c-^i is any point in the ith subinterval, then the sum

(n) Σ (i = 1) [f(c-^i)*Δx-^i],

x-^(i - 1) ≤ c-^i ≤ x-^i

is called a Riemann sum of f for the partition Δ.

norm of a partition - the width of the largest subinterval; denoted by ‖Δ‖

If every subinterval is of equal width, the partition is regular and the norm is denoted by

‖Δ‖ = Δx = (b - a)/n

general partition - the norm is related to the number of subintervals of [a, b]:

(b - a) / ‖Δ‖ ≤ n

‖Δ‖ -> 0 implies n -> ∞

The number of subintervals approaches ∞ as norm approaches 0

THE CONVERSE IS NOT TRUE!

‖Δ‖ -> 0 and n -> ∞ are equivalent in a regular partition

Definition of a Definite Integral:

If f is defined on the closed interval [a, b] and the limit is denoted by

lim (-^- (‖Δ‖ -> 0)) [ (n) Σ (i = 1) [ f(c-^i) * Δx-^i] ]

exists, the f is integrable on [a, b] and the limit is denoted by

lim (-^- (‖Δ‖ -> 0)) [ (n) Σ (i = 1) [ f(c-^i) * Δx-^i] ]

= (∫ a->b) f(x) dx

(The b is supposed to be to the right of ∫ on the upper corner with the a directly below the b in the lower corner to the right of ∫)

The limit is called the definite integral of f from a to b

lower limit of integration - a

upper limit of integration - b

A definite interval is just a value (a number) while an indefinite integral is a family of functions, there's a huge difference!

Theorem 4.4 - Continuity Implies Integrability:

If a function f is continuous on the closed interval [a, b], then f is integrable on [a, b].

Theorem 4.5 - The Definite Integral as the Area of a Region:

If f is continuous and nonnegative on the closed interval [a, b], then the area of the region bounded by the graph of f, the x-axis, and the verticle lines x = a and x = b is given by

Area = (∫ a->b) f(x) dx

NOTE: If the definite integral represents the area of a common geometric region, just use geometric formulas when solving for the area!

Definition of Two Special Definite Integrals:

1. If f is defined at x = a, then we define

(∫ a->b) f(x) dx = 0

2. If f is integrable on [a, b], then we define

(∫ a->b) f(x) dx = -(∫ b->a) f(x) dx

Theorem 4.6 - Additive Interval Property:

If f is integrable on the three closed intervals determined by a, b, and c, then

(∫ a->b) f(x) dx = (∫ a->c) f(x) dx + (∫ c->b) f(x) dx

Theorem 4.7 - Properties of Definite Integrals:

If f and g are integrable on [a, b] and k is a constant, then the functions kf and f ± g are integrable on [a, b], and

1. (∫ a->b) kf(x) dx = k*(∫ a->b) f(x) dx

2. (∫ a->b) [f(x) ± g(x)] dx

= (∫ a->b) f(x) dx ± (∫ a->b) g(x) dx

The second property can be extended to cover any finite number of functions.

Theorem 4.8 - Preservation of Inequality:

1. If f is integrable and nonnegative on the closed interval [a, b], then

0 ≤ (∫ a->b) f(x) dx

2. If f and g are integrable on the closed interval [a, b] and f(x) ≤ g(x) for every x in [a, b], then

(∫ a->b) f(x) dx ≤ (∫ a->b) g(x) dx

Guidelines for Using the Fundamental Theorem of Calculus:

1. Provided you can find an antiderivative of f, you now have a way to evaluate a definite integral without having to use the limit of a sum.

2. When applying the Fundamental Theorem of Calculus, the following notation is convenient:

(∫ a->b) f(x) dx

= F(x) ]`(a ->b)

= F(b) - F(a)

(The a and the b in `(a -> b) goes in the same spots right of ] as it did earlier next to the ∫.)

For instance, to evaluate (∫ 1->3) x^3 dx, you can write

(∫ 1->3) x^3 dx

= ((x^4)/4) ]`(1->3)

= ((3^4)/4) - ((1^4)/4)

=20

3. It is not necessary to include a constant of integration C in the antiderivative because

(∫ a->b) f(x) dx

= [F(x) + C]`(a ->b)

= [F(b) + C] - [F(a) + C]

= F(b) - F(a)

Theorem 4.10 - Mean Value Theorem for Integrals:

If f is continuous on the closed integral [a, b], then there exists a number c in the closed interval [a, b] such that

(∫ a->b) f(x) dx = f(c) * (b - a)

Somewhere between the inscribed and the circumscribed rectangles, there is a rectangle whose are is precisely equal to the area to the region under the curve.

Definition of the Average Value of a Function on an Interval:

If f is integrable on the closed interval [a, b], then the average value of f on the interval is

(1/(b - a)) * (∫ a->b) f(x) dx

The Definite Integral as a Number:

(∫ a->b) f(x) dx

f is a function of x
x is the variable of integration

The Definite Integral as a Function of x:

F(x) = (∫ a->x) f(t) dt

F is a function of x
f is a function of t
t is the variable of integration

The definite integral is NOT a function of its variable of integration!

The interpretation of an integral as an accumulation function is used often in applications of integration.

Theorem 4.11 - The Second Fundamental Theorem of Calculus:

If f is continuous on an open interval I containing a, then for every x in the interval,

d/dx [ (∫ a->x) f(t) dt ] = f(x)

Don't forget the chain rule!

So,

d [ (∫ a->x) f(t) dt = f(x) dx

Chapter 4.4

The Fundamental Theorem of Calculus

Theorem 4.9 - The Fundamental Theorem of Calculus:

If a function f is continuous on the closed interval [a, b] and F is an antiderivative of f on the interval [a, b], then

(∫ a->b) f(x) dx = F(b) - F(a)

Chapter 4.5

Integration by Substitution

Theorem 4.12 - Antidifferentiation of a Composite Function:

Let g be a function whose range is in the interval I, and let f be a function that is continuous on I.

If g is differentiable on its domain and F is an antiderivative of f on I, then

∫ f(g(x)) g′(x) dx = F(g(x)) + C

If u = g(x), then du = g′(x)

and

∫ f(u) du = F(u) + C

Ways to Integrate a Composite Function:

u-substitution - set the variable u to equal a sub-function within the function we are trying to integrate

pattern recognition - recognize which function should be f(x) and which function should be g(x) and then apply Theorem 4.12.

change in variables - use active u-substitution

∫ f(g(x)) g′(x) dx

= ∫ f(u) du = F(u) + C

Guidelines for Making a Change in Variables:

Choose a substitution u = g(x). Usually, it is best to choose the inner part of a composite function, such as a quantity raised to a power.
Compute du = g′(x) dx
Rewrite the integral in terms of the variable u
Find the resulting integral in terms of u
Replace u by g(x) to obtain an antiderivative in terms of x
Check your answer by differentiating.

Theorem 4.13 - The General Power Rule for Integration:

If g is a differentiable function of x, then

∫ ([g(x)]^n) g′(x) dx

= [( ([g(x)]^(n + 1)) ) / (n + 1)] + C,

n ≠ -1

Equivalently, if u = g(x), then

∫ (u^n) du

= ( (u^(n + 1) / (n + 1) ) + C,

n ≠ -1

Change of Variables for Definite Intervals:

If the function u = g(x) has a continuous derivative on the interval [a, b] and f is continuous the range on g, then

(∫ a->b) f(g(x)) g′(x) dx

= (∫ g(a)->g(b)) f(u) du

Theorem 4.14 - Integration of Even and Odd Functions:

Let f be integrable on the closed interval [-a, a].

1. If f is an even function, then

(∫ -a->a) f(x) dx

= 2* (∫ 0->a) f(x) dx

2. If f is an odd function, then

(∫ -a->a) f(x) dx = 0

Chapter 5.1B

The Natural Logarithmic Function

Definition of the Natural Logarithmic Function:

ln x = (∫ 1->x) (1/t) dx,

x > 0

Domain: all positive real numbers

Definition of e:

The letter e denotes the positive real number such that

ln e = (∫ 1->e) (1/t) dx = 1

e is approximately:

2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427427466391932003059921817413596629043572900334295260595630738132328627943490763233829880753195251019011573834187930702154089149934884167509244761460668082264800168477411853742345442437107539077744992069551702761838606261331384583000752044933826560297606737113200709328709127443747047230696977209310141692836819025515108657463772111252389784425056953696770785449969967946864454905987931636889230098793127736178215424999229576351482208269895193668033182528869398496465105820939239829488793320362509443117301238197068416140397019837679320683282376464804295311802328782509819455815301756717361332069811250996181881593041690351598888519345807273866738589422879228499892086805825749279610484198444363463244968487560233624827041978623209002160990235304369941849146314093431738143640546253152096183690888707016768396424378140592714563549061303107208510383750510115747704171898610687396965521267154688957035035402123407849819334321068170121005627880235193033224745015853904730419957777093503660416997329725088687696640355570716226844716256079882651787134195124665...

However, we simply use e = 2.71828182846 in our calculations because the extra digits are not really going to have much of an influence over our calculations. e is a number just like pi (π), there are millions and millions of digits, and there is not much of a point to use ALL of the digits.

Chapter 5.2

The Natural Logarithmic Function: Integration

Theorem 5.5 - Logarithmic Rule for Integration:

Let u be a differentiable function of x.

1. ∫ (1/x) dx = ln |x| + C

2. ∫ (1/u) du = ln |u| + C

∫ (u′/u) dx = ln |u| + C

Guidelines for Integration:

Learn a basic list of integration formulas.
Find an integration formula that resembles part of or all of the integrand, and, by trial and error, find a choice of u that will make the integrand conform to the formula.
If you cannot find a u-substitution that works, try altering the integrand.
If you have access to computer software that will find antiderivatives symbolically, use it! (Unless your teacher wants you to solve the problem without technology.)

Integrals of the Six Basic Trigonometric Functions:

∫ sin u du = -cos u + C

∫ cos u du = sin u + C

∫ tan u du = -ln |cos u| + C

∫ cot u du = ln |sin u| + C

∫ sec u du = ln |sec u + tan u| + C

∫ csc u du = -ln |csc u + cot u| + C

Chapter 5.3

Inverse Functions

Definition of Inverse Functions:

A function g is the inverse function of the function f if

f(g(x)) = x for each x in the domain of g

and

g(f(x)) = x for each x in the domain of f

The function g is denoted f^(-1) (read "f inverse").

If g is the inverse function of f, then f is the inverse function of g.

The domain of f^(-1) is equal to the range of f, and the range of f^(-1) is equal to the domain of f.

A function need not have an inverse function, but if it does, the inverse function is unique.

Theorem 5.6 - Reflective Property of Inverse Functions:

The graph of f contains the point (a, b) if and only if the graph of f^(-1) contains the point (b, a)

Theorem 5.7 - The Existence of an Inverse Function:

1. A function has an inverse function if and only if it is one-to-one.

2. If f is strictly monotonic on its entire domain, then it is one-to-one and therefore has an inverse function.

one-to-one - for every x-value, there is at most one corresponding y-value

strictly monotonic - either increasing or decreasing on the entire interval

horizontal line test - f has an inverse function if and only if every horizontal line intersects it at most once

Guidelines for Finding an Inverse Function:

1. Use Theorem 5.7 to determine whether the function given by y = f(x) has an inverse function.

2. Solve for x as a function of y:

x = g(y) = f^(-1) (y)

3. Interchange x and y. The resulting equation is

y = f^(-1) (x)

4. Define the domain of f^(-1) to be the range of f.

5. Verify that f(f^(-1) (x)) = x and f^(-1) (f(x)) = x

Theorem 5.8 - Continuity and Differentiability of Inverse Functions:

Let f be a function whose domain is an interval I. If f has an inverse function, then the following statements are true.

1. If f is continuous in its domain, then f^(-1) is also continuous in its domain.

2. If f is increasing on its domain, then f^(-1) is also increasing on its domain.

3. If f is decreasing on its domain, then f^(-1) is also decreasing on its domain.

4. If f is differentiable on an interval containing c, and f′(c) ≠ 0, then f^(-1) is differentiable at c.

Theorem 5.9 - The Derivative of an Inverse Function:

Let f be a function that is differentiable on an interval I. If f has an inverse function g, then g is differentiable at any x for which f′(g(x)) ≠ 0. Moreover,

g′(x) = 1/( f′(g(x)) ),

f′(g(x)) ≠ 0

If y = g(x) = f^(-1) (x), then f(y) = x an f′(y) = dx/dy

g′(x)

= dy/dx

= 1/( f′(g(x)) )

= 1/f′(y)

= 1/(dx/dy)

So,

dy/dx = 1/(dx/dy)

Chapter 5.4B

Exponential Functions: Integration

Theorem 5.12 - Integration Rules for Exponential Functions:

Let u be a differentiable function of x.

1. ∫ (e^x) dx = (e^x) + C

2. ∫ (e^x) du = (e^u) + C

Chapter 5.5

Bases Other than e and Applications

Definition of Exponential Function to Base a :

If a is a positive real number (a ≠ 1) and x is any real number, then the exponential function to the base a is denoted by a^x and is defined by

a^x = e^x(ln a)

If a = 1, then y = 1^x = 1 is a constant function.

Definition of Logarithmic Function to Base a:

If a is a positive real number (a ≠ 1) and x is any positive real number, then the logarithmic function to the base a is denoted by log-^a [x] and is defined as

log-^a [x] = ln x / ln a

Properties of Inverse Functions:

1. y = a^x if and only if x = log-^a [y]

2. a^(log-^a [x]) = x, for x > 0

3. log-^a [a^x] = x, for all x

common logarithmic function - has the base of 10

Theorem 5.13 - Derivatives for Bases Other than e:

Let a be a positive real number (a ≠ 1) and let u be a differentiable function of x

1. d/dx [a^x] = (ln a) a^x

2. d/dx [a^u] = (ln a) a^u * (du/dx)

3. d/dx [log-^a [x] ] = 1/(ln a) x

4. d/dx [log-^a [u] ] = (1/(ln a) u) * (du/dx)

Integrals for Bases Other than e:

∫a^x dx

= (1/ln a) a^x + C

You can also use previous definitions and rules to solve an integration function.

Theorem 5.14 - The Power Rule for Real Exponents:

Let n be any real number and let u be a differentiable function of x.

1. d/dx [x^n] = nx^(n -1)

2. d/du [u^n] = nu^(n - 1) * (du/dx)

Theorem 5.15 - A Limit Involving e:

lim (-^- (x -> ∞)) (1 + (1/x))^x

= lim (-^- (x -> ∞)) ((x +1)/x)^x

= e

Summary of Compound Interest Formulas:

P = principle (amount of deposit)
t = time (in years)
A = balance after t years
r = annual interest rate (usually in decimal form)
n = number of compounding per year

1. Compounded n times per year:

A = P (1 + (r/n))^nt

2. Compounded continuously:

A = Pe^rt

Chapter 5.6

Inverse Trigonometric Functions: Differentiation

Definition of Inverse Trigonometric Functions:

y = arcsin x if and only if sin y = x

Domain: -1 ≤ x ≤ 1

Range: -π/2 ≤ y ≤ π/2

y = arccos x if and only if cos y = x

Domain: -1 ≤ x ≤ 1

Range: 0 ≤ y ≤ π

y =arctan x if and only if tan y = x

Domain: -∞ < x < ∞

Range: -π/2 < y < π/2

y = arccsc x if and only if csc y = x

Domain: |x| ≥ 1

Range: -π/2 ≤ y ≤ π/2, y ≠ 0

y = arcsec x if and only if sec y = x

Domain: |x| ≥ 1

Range: 0 ≤ y ≤ π, y ≠ π/2

y = arccot x if and only if cot y = x

Domain: -∞ < x < ∞

Range: 0 < y < π

Properties of Inverse Trigonometric Functions:

If -1 ≤ x ≤ 1 and -π/2 ≤ y ≤ π/2, then

sin (arcsin x) = x

and arcsin (sin y) = y

If -π/2 < y < π/2, then

tan (arctan x) = x

and arctan (tan y) = y

If |x| ≥ 1 and 0 ≤ y < π/2 or π/2 < y < π, then

sec (arcsec x) = x

and arcsec (sec y) = y

Similar properties hold for the other inverse trigonometric functions.

Theorem 5.16 - Derivatives of Inverse Trigonometric Functions:

Let u be a differentiable function of x.

d/dx [arcsin u] = u′/√(1 - u^2)

d/dx [arctan u] = u′/(1 + u^2)

d/dx [arcsec u] = u′/(|u|√(u^2 - 1))

d/dx [arccos u] = -u′/√(1 - u^2)

d/dx [arccot u] = -u′/(1 + u^2)

d/dx [arccsc u] = -u′/(|u|√(u^2 - 1))

Chapter 5.4

Inverse Trigonometric Functions: Integration

Theorem 5.17 - Integrals Involving Inverse Trigonometric Functions:

Let u be a differentiable function of x, and let a > 0.

1. ∫ du/ √(a^2 - u^2)

= arcsin (u/a) + C

2. ∫ du/(a^2 + u^2)

= (1/a) arctan (u/a) + C

3. ∫ du/ u√(u^2 - a^2)

= (1/a) arcsec (|u|/a) + C

It is conventional to use:

arcsin
arctan
arcsec

as the antiderivatives, rather than

-arccos
-arccot
-arccsc